Bayesian uncertainty quantification

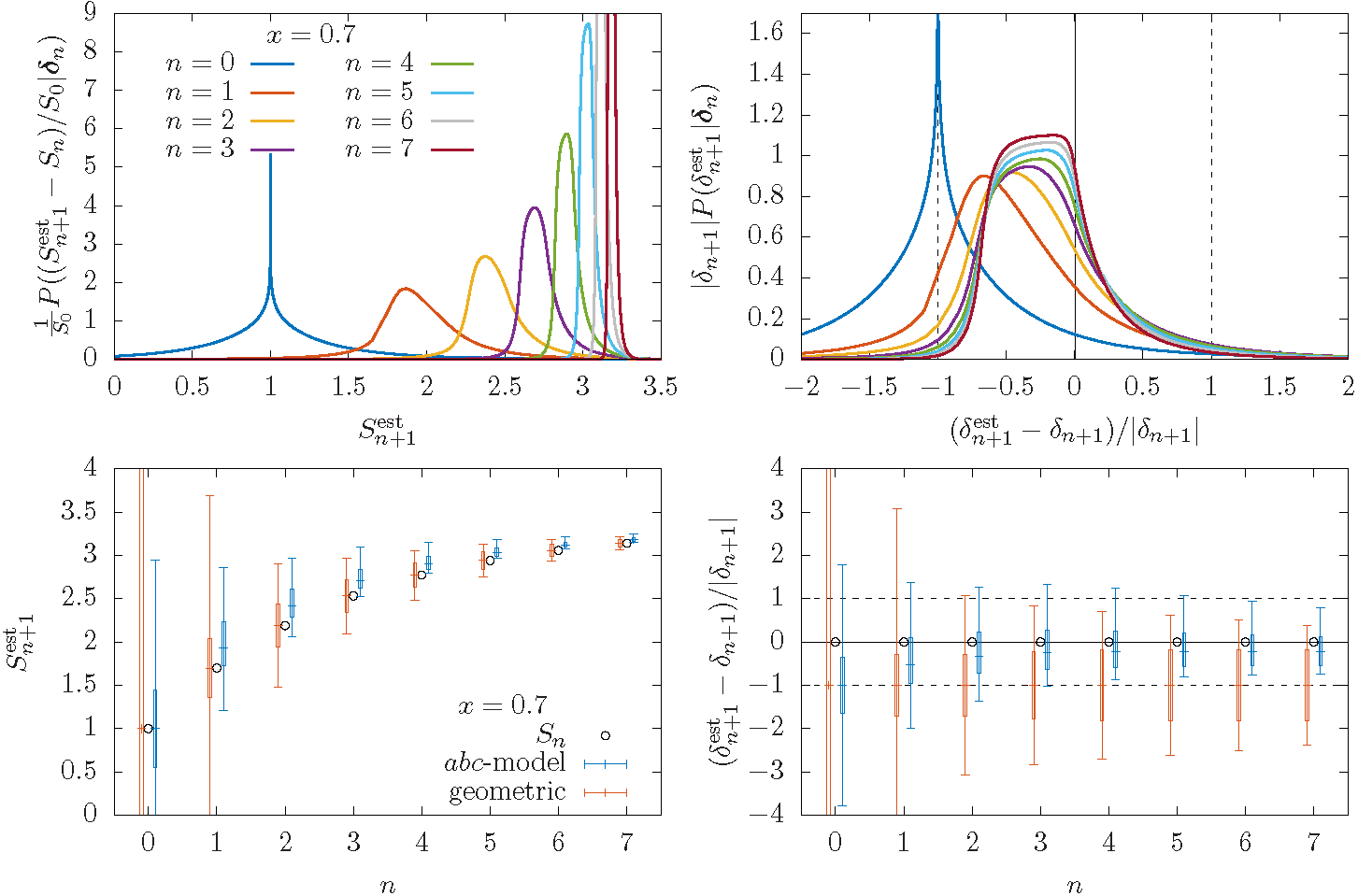
With current high precision collider data, the reliable estimation of theoretical uncertainties due to missing higher orders (MHOs) in perturbation theory has become a pressing issue for collider phenomenology. Traditionally, the size of the MHOs is estimated through scale variation, a simple but ad hoc method without probabilistic interpretation.

Bayesian approaches provide a compelling alternative to estimate the size of the MHOs, but it is not clear how to interpret the perturbative scales, like the factorisation and renormalisation scales, in a Bayesian framework. Recently, it was proposed that the scales can be incorporated as hidden parameters into a Bayesian model. In this paper, we thoroughly scrutinise Bayesian approaches to MHO estimation and systematically study the performance of different models on an extensive set of high-order calculations.

We extend the framework in two significant ways (Duhr et al., 2021). First, we define a new model that allows for asymmetric probability distributions. Second, we introduce a prescription to incorporate information on perturbative scales without interpreting them as hidden model parameters. We clarify how the two scale prescriptions bias the result towards specific scale choice, and we discuss and compare different Bayesian MHO estimates among themselves and to the traditional scale variation approach. Finally, we provide a practical prescription of how existing perturbative results at the standard scale variation points can be converted to 68%/95% credibility intervals in the Bayesian approach using the new public code MiHO.

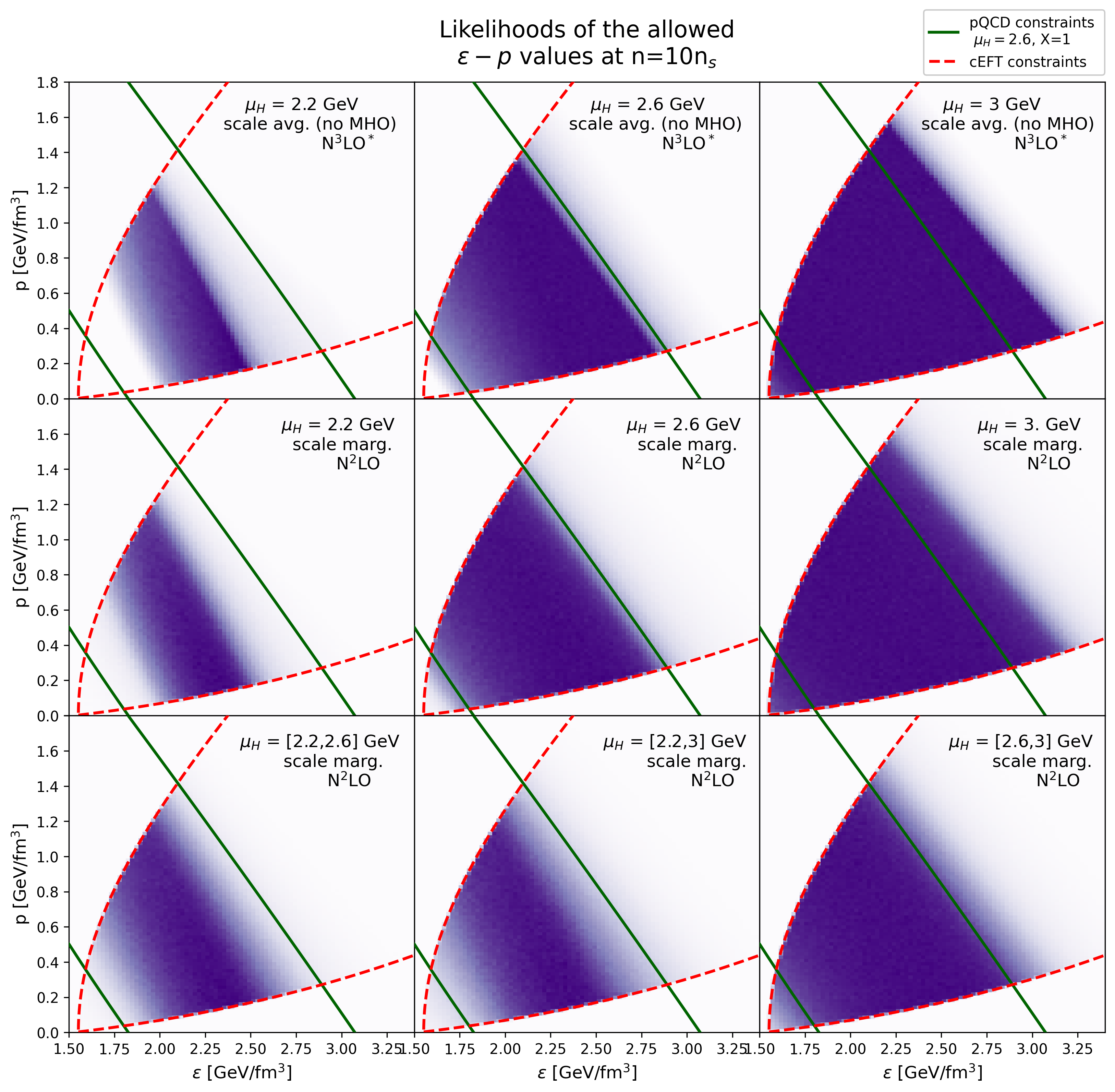
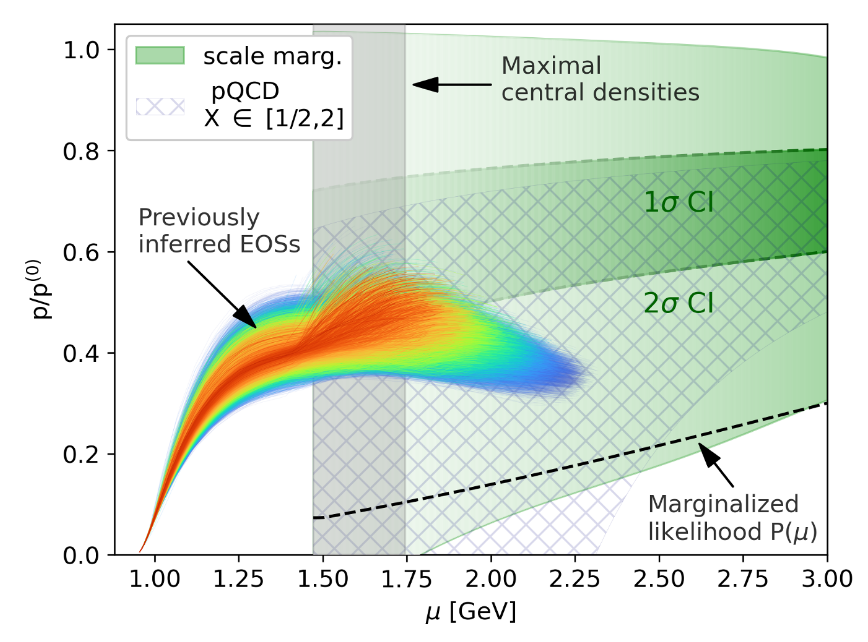
The equation of state of neutron-star cores can be constrained by requiring a consistent connection to the perturbative Quantum Chromodynamics (QCD) calculations at high densities. The constraining power of the QCD input depends on uncertainties from missing higher-order terms, the choice of the unphysical renormalization scale, and the reference density where QCD calculations are performed. Within a Bayesian approach, we discuss the convergence of the perturbative QCD series, quantify its uncertainties at high densities, and present a framework to systematically propagate the uncertainties down to neutron-star densities (Gorda et al., 2023).