A kinetic regime of hydrodynamic fluctuations and long time tails for a Bjorken expansion

Abstract

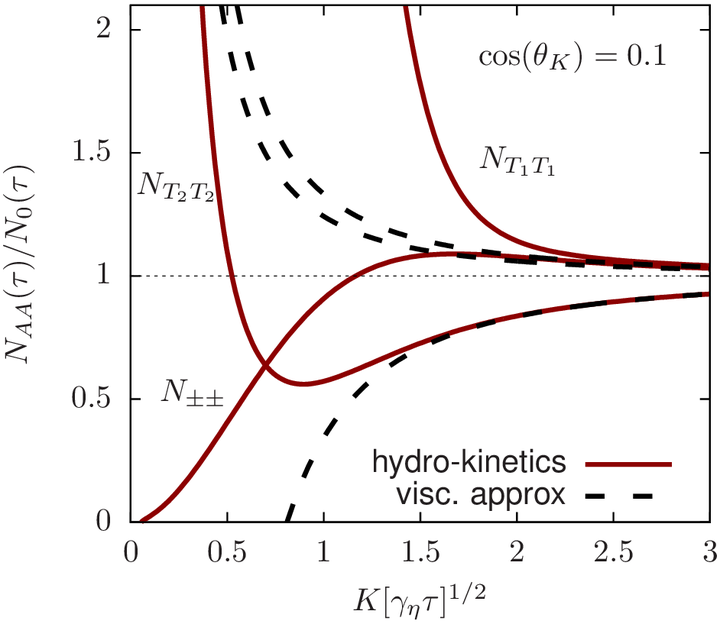
We develop a set of kinetic equations for hydrodynamic fluctuations which are equivalent to nonlinear hydrodynamics with noise. The hydrokinetic equations can be coupled to existing second-order hydrodynamic codes to incorporate the physics of these fluctuations. We first show that the kinetic response precisely reproduces the renormalization of the shear viscosity and the fractional power (∝ω3/2) which characterizes equilibrium correlators of energy and momentum for a static fluid. Then we use the hydrokinetic equations to analyze thermal fluctuations for a Bjorken expansion, evaluating the contribution of thermal noise from the earliest moments and at late times. In the Bjorken case, the solution to the kinetic equations determines the coefficient of the first fractional power of the gradient expansion (∝1/(τT)3/2) for the expanding system. Numerically, we find that the contribution to the longitudinal pressure from hydrodynamic fluctuations is larger than second-order hydrodynamics for typical medium parameters used to simulate heavy ion collisions.