An analysis of Bayesian estimates for missing higher orders in perturbative calculations
Abstract
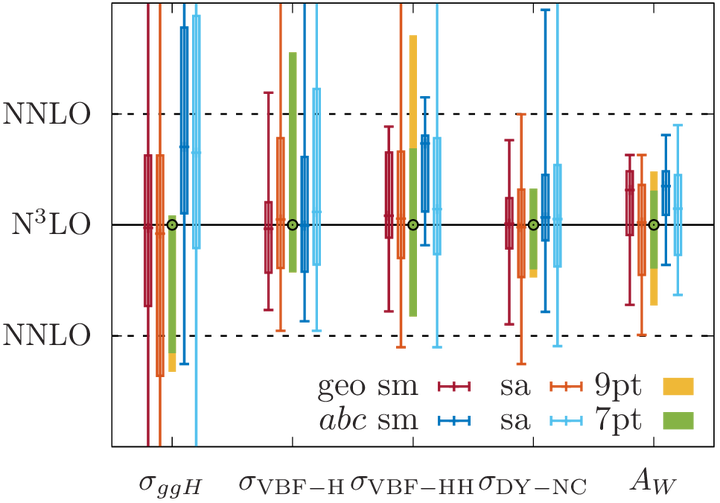
With current high precision collider data, the reliable estimation of theoretical uncertainties due to missing higher orders (MHOs) in perturbation theory has become a pressing issue for collider phenomenology. Traditionally, the size of the MHOs is estimated through scale variation, a simple but ad hoc method without probabilistic interpretation. Bayesian approaches provide a compelling alternative to estimate the size of the MHOs, but it is not clear how to interpret the perturbative scales, like the factorisation and renormalisation scales, in a Bayesian framework. Recently, it was proposed that the scales can be incorporated as hidden parameters into a Bayesian model. In this paper, we thoroughly scrutinise Bayesian approaches to MHO estimation and systematically study the performance of different models on an extensive set of high-order calculations. We extend the framework in two significant ways. First, we define a new model that allows for asymmetric probability distributions. Second, we introduce a prescription to incorporate information on perturbative scales without interpreting them as hidden model parameters. We clarify how the two scale prescriptions bias the result towards specific scale choice, and we discuss and compare different Bayesian MHO estimates among themselves and to the traditional scale variation approach. Finally, we provide a practical prescription of how existing perturbative results at the standard scale variation points can be converted to 68%/95% confidence intervals in the Bayesian approach using the new public code MiHO.