Bayesian uncertainty quantification of perturbative QCD input to the neutron-star equation of state
Abstract
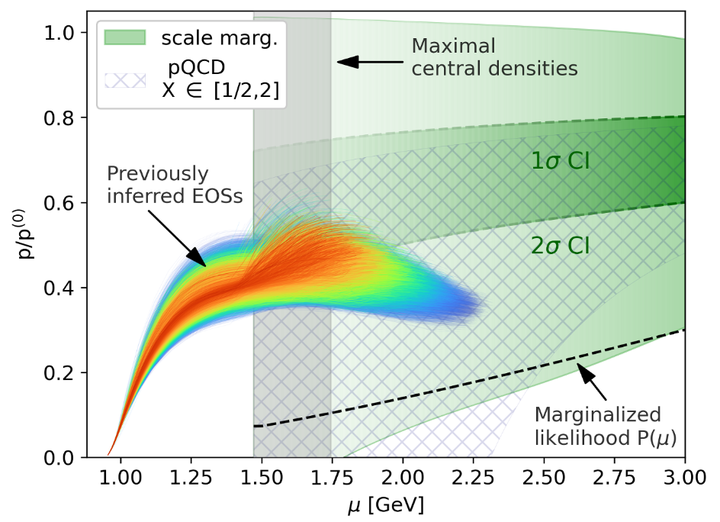
The equation of state of neutron-star cores can be constrained by requiring a consistent connection to the perturbative Quantum Chromodynamics (QCD) calculations at high densities. The constraining power of the QCD input depends on uncertainties from missing higher-order terms, the choice of the unphysical renormalization scale, and the reference density where QCD calculations are performed. Within a Bayesian approach, we discuss the convergence of the perturbative QCD series, quantify its uncertainties at high densities, and present a framework to systematically propagate the uncertainties down to neutron-star densities. We find that the effect of the QCD input on the neutron-star inference is insensitive to the various unphysical choices made in the uncertainty estimation.